CD Units FAQs
- Circular dichroism data is commonly expressed in terms of a differential absorbance, a molar circular dichroism, or ellipticity.
- As explained in the Circular Dichroism FAQs, circular dichroism is a differential absorbance, i.e., the difference in absorbance of left-handed circularly polarised (L-CP) light and right-handed circularly polarised (R-CP) light:
CD = ΔA = AL-CP - AR-CP
- As CD spectroscopy is an absorbance technique, the Beer-Lambert law applies the same way as it does for UV/Vis absorbance spectroscopy. For CD spectroscopy, it becomes:
∆A = ∆ε ∙ c ∙ l
where c is the molar compound concentration (in M), l is the cell pathlength (in cm), and Δε = εL-CP – εR-CP is the molar circular dichroism (in M-1 cm-1) with εL-CP and εR-CP being the molar extinction coefficients for L-CP and R-CP light, respectively.
For many biochemists, ΔA and Δε are the most intuitive approaches to reporting CD data, as they are derived from the familiar concept of UV/Vis absorbance spectroscopy, and also directly relate to how modern CD instruments actually measure circular dichroism.
- However, in the literature, CD data is still most commonly expressed as degrees of ellipticity, θ. The advantage of reporting data in terms of ellipticity is that it is more easily related to optical rotation measurements and polarimetry. Both ellipticity and optical rotation are measurements of changes in the polarisation state of a linearly polarised analyser beam, and both have the same units and similar amplitudes for a given sample. This similarity aids in the comparison of optical rotation and CD measurements, a useful ability when CD spectroscopy first started to be widely used in the 1960's.
- The description of ellipticity is somewhat more complex than that of ΔA. Linearly polarised light (purple in the animation below), when passed through a circular dichroic sample (green box in the animation below), will become elliptically polarised.
- Linearly polarised light can be described as a combination of a left-handed (blue in the animation below) and a right-handed (gray in the animation below) circularly polarised component of equal amplitude. The lineraly polarised light becomes elliptically polarised when the magnitudes of the two components become different due to differential absorbance.
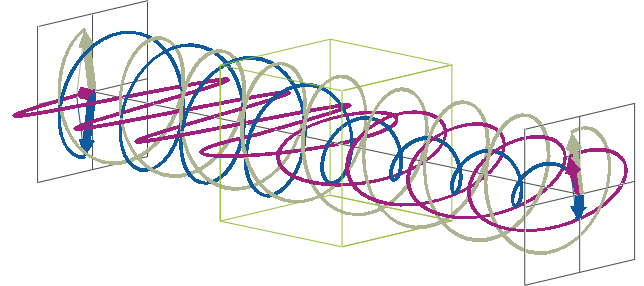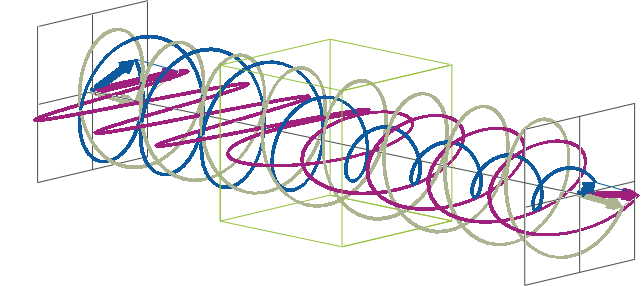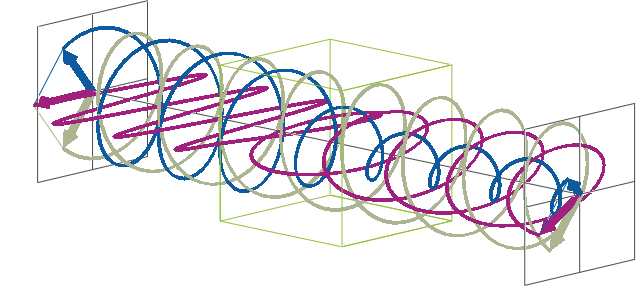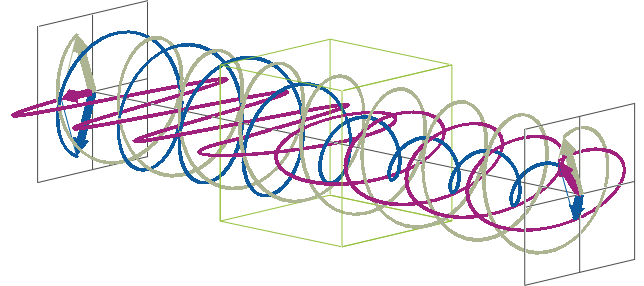
- The ellipse of the elliptically polarised light can be described by the lengths of its major and minor axes:
- The length of the major axis is the sum of the magnitudes of the electric field vectors of the R- and L-CP light, ER + EL.
- The length of the minor axis is the difference between the magnitudes of the electric field vectors of the R- and L-CP light, ER - EL.
The degree of ellipticity is then defined as the tangent of the angle θ, which is equal to the ratio of the minor to major elliptical axis:
tan θ = (ER - EL) / (ER + EL) ≈ θ
The degree of ellipticity is 0° for linearly polarised light (ER = EL) , while it is +45° (ER = 0) and -45° (EL = 0) for L- or R-CP light, respectively.
As the difference in absorbances of L- and R-CP light is typically very small, tan θ can be approximated as θ (in radians).
- By taking into account that light intensity is proportional to the square of the electric field vector, using the Beer-Lambert law, and converting from radians to degrees, additional calculations result in a direct relationship between θ (in degrees) and the differential absorbance:
θ (degrees) = ∆A (ln 10 / 4) (180 / π) ≈ ∆A ∙ 32.982
Due to the small magnitude of CD signals in most measurements, θ is often quoted as millidegrees (m˚), i.e., 1/1000 of a degree.
- To be able to compare CD results that have been obtained with different experimental setups, ellipticity is often reported as molar ellipticity, [θ], which normalizes the ellipticity to pathlength and concentration and refers to a pathlength in meters rather than centimeters (which introduces a factor of 100). It follows that molar ellipticity is:
[θ] = 100 ∙ θ / (l ∙ c)
with [θ] in deg M-1 m-1, θ in deg, c in M, and l in cm.
Following polarimetric conventions, [θ] is often expressed in deg cm2 dmol-1. In fact, this unit it equivalent to deg M-1 m-1:
M-1 m-1 = 1000 (cm3 / l) ∙ (mol / 10 dmol) ∙ (l / mol) ∙ (1 / m) ∙ (m / 100 cm)
= 1000 (cm32 / l) ∙ (mol / 10 dmol) ∙ (l / mol) ∙ (1 / m) ∙ (m / 100 cm)
= cm2 dmol-1
Molar circular dichroism and molar ellipticity can be converted directly by:
[θ] = Δε ∙ 3298.2
This factor is a hundred fold larger than for the conversion between differential absorbance and ellipticity because path length is defined in centimeters for molar extinction and in meters for ellipticity.
- Proteins with different molecular weights can yield far-UV CD spectra of vastly different magnitudes even if they have a similar overall secondary structure and samples of similar molar concentrations are used. In such cases, CD data obtained for different proteins can easily be compared using the mean residue molar ellipticity, [θ]MR, which reports the molar circular dichroism for individual protein residues instead of whole protein molecules.
There are two ways to calculate [θ]MR depending on whether the sequence of the protein and, thus, the number of amino acids, N, in the protein is known or not:
- If N is known:
[θ]MR = 100 ∙ θ / (l ∙ c ∙ N) = 3298.2 ∙ ∆εMR = 3298.2 ∙ ∆A / (l ∙ c ∙ N)
where cMR = c ∙ N is the mean residue concentration. [θ]MR is just [θ] normalized by the number of amino acids in the protein.
- If N is not known:
[θ]MR = 100 ∙ θ / (l ∙ C) ∙ 110 = 3298.2 ∙ ∆εMR = 3298.2 ∙ ∆A / (l ∙ C) ∙ 110
where CMR = C / 110 is an estimate of the mean residue concentration that is calculated by using the protein’s mass concentration C in mg/mL instead of its molar concentration, and the average molecular weight of amino acids, 110 da.


